Покомпонентная функция когерентности взаимосвязанных периодически нестационарных случайных процессов

Автор(и)

  • Игорь Николаевич Яворский Физико-механический институт им. Г. В. Карпенко Национальной Академии наук Украины; Институт телекоммуникаций технологически-естествоведческого университета, Україна https://orcid.org/0000-0002-6533-3186
  • Роман Михайлович Юзефович Физико-механический институт им. Г. В. Карпенко Национальной Академии наук Украины, Україна https://orcid.org/0000-0001-5546-453X
  • Иван Иосифович Мацько Физико-механический институт им. Г. В. Карпенко Национальной Академии наук Украины, Україна
  • Збигнев Закжевски Институт телекоммуникаций технологически-естествоведческого университета, Польща

DOI:

https://doi.org/10.20535/S0021347017010046

Ключові слова:

периодически нестационарный случайный процесс, модулирующие стационарно связанные случайные процессы, линейные преобразования, амплитудно-модулированный сигнал, фазомодулированный сигнал

Анотація

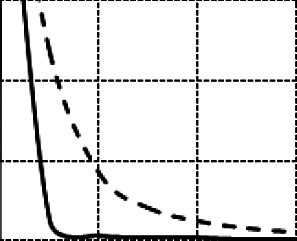
Рассмотрена новая покомпонентная функция когерентности, которая определяется взаимоспектральными плотностями стационарных компонентов периодически нестационарных случайных сигналов — стационарно связанных случайных процессов, модулирующих их несущие гармоники. Свойства введенной функции когерентности конкретизированы для амплитудно- и фазомодулированных сигналов, получены ее графические частотные зависимости для заданных параметров сигналов. Показаны преимущества покомпонентной функции когерентности в сравнении с ранее введенной интегральной функцией когерентности. Приведен метод выделения стационарных модулирующих компонентов, который основан на частотном сдвиге и низкочастотной фильтрации. Проанализированы свойства выделяемых компонентов в случае амплитудных и фазовых модуляций.

Посилання

Bendat, J. S.; Piersol, A. G. Random Data: Analysis and Measurement Procedures. — New York : John Wiley @ Sons, 2010. — 640 p.

Kay, S. Modern Spectral Estimation: Theory and Application. New Jersey : Prentise Hall, 1987. — 543 p.

Яворський, І. М. Математичні моделі та аналіз стохастичних коливань. Під заг. ред. З. Т. Назарчука. — Львів : ФМІ НАНУ, 2013. — 804 с.

Яворський, І. М.; Кравець, І. Б.; Юзефович, Р. М. Взаємоз періодично корельовані випадкові процеси. Відбір і обробка інформації. — 2011. — № 34. — С. 69–77.

Яворский, И. Н.; Юзефович, Р. М.; Мацько, И. Й.; Закжевски, З. Функция когерентности взаимосвязанных периодически нестационарных случайных процессов. Известия вузов. Радиоэлектроника. — 2016. — Т. 59, № 3. — C. 40–51. — DOI : http://dx.doi.org/10.20535/S0021347016030043.

Gardner, W. A. Eexploitation of spectral redundancy in cyclostationary signals. IEEE SP Magazine (Signal Processing). — Apr. 1991. — Vol. 8, No. 2. — P. 14–36. — DOI : http://dx.doi.org/10.1109/79.81007.

Gardner, W. A. (ed.). Cyclostationarity in Communications and Signal Processing. — New York : IEEE Press, 1994. — 504 p.

Hurd, H. L.; Miamee, A. Periodically Сorrelated Random Sequences. Spectral Theory and Practice. — New Jersey : Wiley-Interscience, 2007. — 353 p.

Napolitano, A. Cyclostationarity: New trends and applications. Signal Processing. — Mar. 2016. — Vol. 120. — P. 385–408. — DOI : http://dx.doi.org/10.1016/j.sigpro.2015.09.011.

Obuchowski, J.; Wylomanska, A.; Zimroz, R. Identification of cyclic components in presence of non-Gaussian noise — application to crusher bearings damage detection. J. Vibroengineering. — 2015. — Vol. 17, No. 3. — P. 1242–1252. — URL : http://www.jve.lt/Vibro/JVE-2015-17-3/JVE01715051589.html.

Obuchowski, J.; Wylomanska, A.; Zimroz, R. The local maxima method for enhancement of time-frequency map and its application to local damage detection in rotating machines. Mechanical Systems and Signal Processing. — Jun. 2014. — Vol. 46, No. 2. — P. 389–405. — DOI : http://dx.doi.org/10.1016/j.ymssp.2014.01.009.

Javorskyj, I.; Leskow, J.; Kravets, I.; Isayev, I.; Gajecka, E. Linear filtration methods for statistical analysis of periodically correlated random processes—Part II: Harmonic series representation. Signal Processing. — Nov. 2011. — Vol. 91, No. 11. — P. 2506–2519. — DOI : http://dx.doi.org/10.1016/j.sigpro.2011.04.031.

##submission.downloads##

Опубліковано

2017-01-15

Як цитувати

Яворский, И. Н., Юзефович, Р. М., Мацько, И. И., & Закжевски, З. (2017). Покомпонентная функция когерентности взаимосвязанных периодически нестационарных случайных процессов. Вісті вищих учбових закладів. Радіоелектроніка, 60(1), 37–49. https://doi.org/10.20535/S0021347017010046

Номер

Том 60 № 1 (2017)

Розділ

Оригінальні статті

Ліцензія

Авторське право (c) 2017 Известия высших учебных заведений. Радиоэлектроника

Издатель журнала Известия высших учебных заведений. Радиоэлектроника (сокр. "Известия вузов. Радиоэлектроника"), Национальный технический университет Украины "Киевский политехнический институт", учитывает, что доступ автора к его статье является важным как для самого автора, так и для спонсоров его исследований. Мы представлены в базе издателей SHERPA/RoMEO как зеленый издатель (green publisher), что позволяет автору выполнять самоархивирование своей статьи. Однако важно, чтобы каждая из сторон четко понимала свои права. Просьба более детально ознакомиться с Политикой самоархивирования нашего журнала.

Политика оплаченного открытого доступа POA (paid open access), принятая в журнале, позволяет автору выполнить все необходимые требования по открытому доступу к своей статье, которые выдвигаются институтом, правительством или фондом при выделении финансирования. Просьба более детально ознакомиться с политикой оплаченного открытого доступа нашего журнала (см. отдельно).

Варианты доступа к статье:

1. Статья в открытом доступе POA (paid open access)

В этом случае права автора определяются лицензией CC BY (Creative Commons Attribution).

2. Статья с последующим доступом по подписке

В этом случае права автора определяются авторским договором, приведенным далее.

  • Автор (каждый соавтор) уступает Издателю журнала «Известия высших учебных заведений. Радиоэлектроника» НТУУ «КПИ» на срок действия авторского права эксклюзивные права на материалы статьи, в том числе право на публикацию данной статьи издательством Аллертон Пресс, США (Allerton Press) на английском языке в журнале «Radioelectronics and Communications Systems». Передача авторского права охватывает исключительное право на воспроизведение и распространение статьи, включая оттиски, переводы, фото воспроизведения, микроформы, электронные формы (он- и оффлайн), или любые иные подобные формы воспроизведения, а также право издателя на сублицензирование третьим лицам по своему усмотрению без дополнительных консультаций с автором. При этом журнал придерживается Политики конфиденциальности.
  • Передача прав включает право на обработку формы представления материалов с помощью компьютерных программам и систем (баз данных) для их использования и воспроизводства, публикации и распространения в электронном формате и внедрения в системы поиска (базы данных).
  • Воспроизведение, размещение, передача или иное распространение или использование материалов, содержащихся в статье должно сопровождаться ссылкой на Журнал и упоминанием Издателя, а именно: название статьи, имя автора (соавторов), название журнала, номер тома, номер выпуска, копирайт авторов и издателя "© Национальный технический университет Украины "Киевский политехнический институт"; © автор(ы)".
  • Автор (каждый соавтор) материалов сохраняет все права собственника материалов, включая патентные права на любые процессы, способы или методы и др., а также права на товарные знаки.
  • Издатель разрешает автору (каждому соавтору) материалов следующее:
  1. Право пользоваться печатными или электронными вариантами материалов статьи в форме и содержании, принятыми Издателем для публикации в Журнале. Подробнее см. политики Оплаченного открытого доступа, подписки и самоархивирования.
  2. Право бесплатно копировать или передавать коллегам копию напечатанной статьи целиком или частично для их личного или профессионального использования, для продвижения академических или научных исследований или для учебного процесса или других информационных целей, не связанных с коммерческими целями.
  3. Право использовать материалы из опубликованной статьи в написанной автором (соавторами) книге, монографии, учебнике, учебном пособии и других научных и научно-популярных изданиях.
  4. Право использовать отдельные рисунки или таблицы и отрывки текста из материалов в собственных целях обучения или для включения их в другую работу, которая печатается (в печатном или электронном формате) третьей стороной, или для представления в электронном формате во внутренние компьютерные сети или на внешние сайты автора (соавторов).
  • Автор (соавторы) соглашаются, что каждая копия материалов или любая ее часть, распространенная или размещенная ими в печатном или электронном формате, будет содержать указание на авторское право, предусмотренное в Журнале и полную ссылку на Журнал Издателя.
  • Автор (соавторы) гарантирует, что материалы являются оригинальной работой и представлены впервые на рассмотрение только в этом Журнале и ранее не публиковались. Если материалы написаны совместно с соавторами, автор гарантирует, что проинформировал их относительно условий публикации материалов и получил их подписи или письменное разрешение подписываться от их имени.
  • Если в материалы включаются отрывки из работ или имеются указания на работы, которые охраняются авторским правом и принадлежат третьей стороне, то автору необходимо получить разрешение владельца авторских прав на использование таких материалов в первом случае и сделать ссылку на первоисточник во втором.
  • Автор гарантирует, что материалы не содержат клеветнических высказываний и не посягают на права (включая без ограничений авторское право, права на патент или торговую марку) других лиц и не содержат материалы или инструкции, которые могут причинить вред или ущерб третьим лицам. Автор (каждый соавтор) гарантирует, что их публикация не приведет к разглашению секретных или конфиденциальных сведений (включая государственную тайну). Подтверждением этого является Экспертное заключение (см. перечень документов в Правила для авторов).
  • Издатель обязуется опубликовать материалы в случае получения статьей положительного решения редколлегии о публикации на основании внешнего рецензирования (см. Политика рецензирования).
  • В случае публикации статьи на английском языке в журнале «Radioelectronics and Communications Systems» (Издатель: Аллертон Пресс, США, распространитель Springer) автору (соавторам) выплачивается гонорар после выхода последнего номера журнала года, в котором опубликована данная статья.
  • Документ Согласие на публикацию, который подают русскоязычные авторы при подаче статьи в редакцию, является краткой формой данного договора, в котором изложены все ключевые моменты настоящего договора и наличие которого подтверждает согласие автора (соавторов) с ним. Аналогичным документом для англоязычных авторов является Copyright Transfer Agreement (CTA), предоставляемый издательством Allerton Press.
  • Настоящий Договор вступает в силу в момент принятия статьи к публикации. Если материалы не принимаются к публикации или до публикации в журнале автор (авторы) отозвал работу, настоящий Договор не приобретает (теряет) силу.