Проста методика визначення довжин закритичних зон біконічного резонатора
DOI:
https://doi.org/10.20535/S0021347024010011Ключові слова:
біконічний резонатор, метод колокації, розкладання за власними функціями, закритична зона, частково перетинні областіАнотація
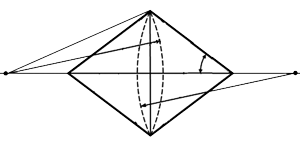
У роботі представлено просту методику визначення довжини закритичних зон поблизу кінців біконічного резонатора, де отвори для введення зразків можуть бути зроблені без суттєвого спотворення резонансних частот і структури поля. Методика використовує метод частково перетинних областей у комбінації з методом колокації. Внутрішність резонатора поділено на дві перетинні області, на межах яких задано точки колокації. У кожній області електричне поле представлено у вигляді розкладу за власними функціями, та з умови рівності електричних полів в обох областях у точках колокації отримано однорідну систему лінійних рівнянь відносно коефіцієнтів розкладання. Коефіцієнти розкладання визначено як власний вектор матриці цієї системи, що відповідає її нульовому власному значенню. За допомогою знайдених коефіцієнтів розкладання розраховано розподіл електричного поля, нормований на максимальне електричне поле в резонаторі, що дозволяє знайти довжину закритичних зон, означених як області, де електричне поле не перевищує заданої малої частки максимального електричного поля в резонаторі. Оскільки всього чотири пари точок колокації виявилися достатніми, обсяг обчислень для запропонованоi методики є досить помірним, що дозволяє використовувати її при розробці вимірювачів на основі біконічних резонаторів з відкритими кінцями.
Посилання
- R. I. Bilous, A. P. Motornenko, “Comparison of characteristics of resonator on the basis of evanescent waveguides in millimeter wavelength band,” Telecommun. Radio Eng., vol. 66, no. 15, pp. 1365–1369, 2007, doi: https://doi.org/10.1615/TelecomRadEng.v66.i15.30.
- S. M. Jensen, R. B. Bass, A. W. Lichtenberger, A. M. Datesman, “A simple GHz resonator for superconducting materials characterization,” IEEE Trans. Appl. Supercond., vol. 25, no. 3, pp. 1–4, 2015, doi: https://doi.org/10.1109/TASC.2014.2379285.
- A. Rashidian, L. Shafai, D. Klymyshyn, C. Shafai, “A fast and efficient free-space dielectric measurement technique at mm-wave frequencies,” IEEE Antennas Wirel. Propag. Lett., vol. 16, pp. 2630–2633, 2017, doi: https://doi.org/10.1109/LAWP.2017.2737632.
- M. V. Andreev, O. O. Drobakhin, Y. N. Privalov, D. Y. Saltykov, “Measurement of dielectric material properties using coupled biconical resonators,” Telecommun. Radio Eng., vol. 73, no. 11, pp. 1017–1032, 2014, doi: https://doi.org/10.1615/TelecomRadEng.v73.i11.70.
- О. О. Дробахин, П. И. Заболотный, Е. Н. Привалов, “Учет влияния элементов связи на резонансные явления в биконических резонаторах,” Известия вузов. Радиоэлектроника, vol. 53, no. 7, pp. 56–63, 2010, doi: https://doi.org/10.20535/S0021347010070071.
- O. O. Drobakhin, Y. N. Privalov, D. Y. Saltykov, “Open-ended waveguide cutoff resonators for monitoring dielectrics parameters of gases,” Telecommun. Radio Eng., vol. 72, no. 7, pp. 627–640, 2013, doi: https://doi.org/10.1615/TelecomRadEng.v72.i7.60.
- P. Zabolotnyi, “Open-ended microwave biconical cavity for the determination of the average electron density in a low-temperature plasma,” in 2022 IEEE 2nd Ukrainian Microwave Week (UkrMW), 2022, pp. 131–134, doi: https://doi.org/10.1109/UkrMW58013.2022.10037160.
- B. Z. Katsenelenbaum, L. Mercader del Rio, M. Pereyaslavets, M. Sorolla Ayza, M. Thumm, Theory of Nonuniform Waveguides: The Cross-Section Method. London: IET, 1998, doi: https://doi.org/10.1049/PBEW044E.
- J. P. Van’t Hof, D. D. Stancil, “Eigenfrequencies of a truncated conical resonator via the classical and Wentzel–Kramers–Brillouin methods,” IEEE Trans. Microw. Theory Tech., vol. 56, no. 8, pp. 1909–1916, 2008, doi: https://doi.org/10.1109/TMTT.2008.927408.
- P. Zabolotnyy, “On the study of the resonant properties of a biconical cavity with a dielectric rod using the quasiregular approximation method,” in 2014 International Conference on Mathematical Methods in Electromagnetic Theory, 2014, pp. 172–175, doi: https://doi.org/10.1109/MMET.2014.6928759.
- К. Г. Савин, И. П. Голубева, Ю. В. Прокопенко, “Расчет частотных и энергетических характеристик составного металло-диэлектрического резонатора методом частичных областей,” Известия вузов. Радиоэлектроника, vol. 59, no. 5, p. 47, 2016, doi: https://doi.org/10.20535/S0021347016050058.
- D. B. Kuryliak, Z. T. Nazarchuk, O. B. Trishchuk, “Axially-symmetric TM-waves diffraction by sphere-conical cavity,” Prog. Electromagn. Res. B, vol. 73, pp. 1–16, 2017, doi: https://doi.org/10.2528/PIERB16120904.
- О. О. Дробахин, П. И. Заболотный, Е. Н. Привалов, “К приближенному расчету собственных частот биконических микроволновых резонаторов,” Известия вузов. Радиоэлектроника, vol. 56, no. 3, pp. 28–35, 2013, doi: https://doi.org/10.20535/S0021347013030035.
- S. A. Kostylev, E. F. Prokhorov, N. B. Gorev, I. F. Kodzhespirova, Y. A. Kovalenko, “Low-frequency capacitance–voltage characterization of deep levels in film–buffer layer–substrate GaAs structures,” Solid-State Electron., vol. 43, no. 1, pp. 169–176, 1999, doi: https://doi.org/10.1016/S0038-1101(98)00189-0.
- R. H. W. Hoppe, Y. A. Kuznetsov, “Overlapping domain decomposition methods with distributed Lagrange multipliers,” J. Numer. Math., vol. 9, no. 4, 2001, doi: https://doi.org/10.1515/JNMA.2001.285.
- М. В. Андреев, О. О. Дробахин, Д. Ю. Салтыков, Н. Б. Горев, И. Ф. Коджеспирова, “Простой метод определения собственных частот биконического резонатора,” Известия вузов. Радиоэлектроника, vol. 60, no. 12, pp. 717–725, 2017, doi: https://doi.org/10.20535/S0021347017120056.
- М. В. Андреев, О. О. Дробахин, Д. Ю. Салтыков, Н. Б. Горев, И. Ф. Коджеспирова, “Определение собственных частот биконического резонатора методом частичных пересекающихся областей с использованием дробно-рациональной аппроксимации,” Известия вузов. Радиоэлектроника, vol. 62, no. 12, pp. 737–749, 2019, doi: https://doi.org/10.20535/S0021347019120033.
- O. O. Drobakhin, “Prony’s-method identification of parameters of model which is sum of exponential functions,” Optoelectron. Instrumentation, Data Process., no. 4, pp. 37–42, 1989.
- T. K. Sarkar, M. Salazar-Palma, M. Da Zhu, H. Chen, Modern Characterization of Electromagnetic Systems and Its Associated Metrology. Wiley-IEEE Press, 2021.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Вісті вищих учбових закладів. РадіоелектронікаИздатель журнала Известия высших учебных заведений. Радиоэлектроника (сокр. "Известия вузов. Радиоэлектроника"), Национальный технический университет Украины "Киевский политехнический институт", учитывает, что доступ автора к его статье является важным как для самого автора, так и для спонсоров его исследований. Мы представлены в базе издателей SHERPA/RoMEO как зеленый издатель (green publisher), что позволяет автору выполнять самоархивирование своей статьи. Однако важно, чтобы каждая из сторон четко понимала свои права. Просьба более детально ознакомиться с Политикой самоархивирования нашего журнала.
Политика оплаченного открытого доступа POA (paid open access), принятая в журнале, позволяет автору выполнить все необходимые требования по открытому доступу к своей статье, которые выдвигаются институтом, правительством или фондом при выделении финансирования. Просьба более детально ознакомиться с политикой оплаченного открытого доступа нашего журнала (см. отдельно).
Варианты доступа к статье:
1. Статья в открытом доступе POA (paid open access)
В этом случае права автора определяются лицензией CC BY (Creative Commons Attribution).
2. Статья с последующим доступом по подписке
В этом случае права автора определяются авторским договором, приведенным далее.
- Автор (каждый соавтор) уступает Издателю журнала «Известия высших учебных заведений. Радиоэлектроника» НТУУ «КПИ» на срок действия авторского права эксклюзивные права на материалы статьи, в том числе право на публикацию данной статьи издательством Аллертон Пресс, США (Allerton Press) на английском языке в журнале «Radioelectronics and Communications Systems». Передача авторского права охватывает исключительное право на воспроизведение и распространение статьи, включая оттиски, переводы, фото воспроизведения, микроформы, электронные формы (он- и оффлайн), или любые иные подобные формы воспроизведения, а также право издателя на сублицензирование третьим лицам по своему усмотрению без дополнительных консультаций с автором. При этом журнал придерживается Политики конфиденциальности.
- Передача прав включает право на обработку формы представления материалов с помощью компьютерных программам и систем (баз данных) для их использования и воспроизводства, публикации и распространения в электронном формате и внедрения в системы поиска (базы данных).
- Воспроизведение, размещение, передача или иное распространение или использование материалов, содержащихся в статье должно сопровождаться ссылкой на Журнал и упоминанием Издателя, а именно: название статьи, имя автора (соавторов), название журнала, номер тома, номер выпуска, копирайт авторов и издателя "© Национальный технический университет Украины "Киевский политехнический институт"; © автор(ы)".
- Автор (каждый соавтор) материалов сохраняет все права собственника материалов, включая патентные права на любые процессы, способы или методы и др., а также права на товарные знаки.
- Издатель разрешает автору (каждому соавтору) материалов следующее:
- Право пользоваться печатными или электронными вариантами материалов статьи в форме и содержании, принятыми Издателем для публикации в Журнале. Подробнее см. политики Оплаченного открытого доступа, подписки и самоархивирования.
- Право бесплатно копировать или передавать коллегам копию напечатанной статьи целиком или частично для их личного или профессионального использования, для продвижения академических или научных исследований или для учебного процесса или других информационных целей, не связанных с коммерческими целями.
- Право использовать материалы из опубликованной статьи в написанной автором (соавторами) книге, монографии, учебнике, учебном пособии и других научных и научно-популярных изданиях.
- Право использовать отдельные рисунки или таблицы и отрывки текста из материалов в собственных целях обучения или для включения их в другую работу, которая печатается (в печатном или электронном формате) третьей стороной, или для представления в электронном формате во внутренние компьютерные сети или на внешние сайты автора (соавторов).
- Автор (соавторы) соглашаются, что каждая копия материалов или любая ее часть, распространенная или размещенная ими в печатном или электронном формате, будет содержать указание на авторское право, предусмотренное в Журнале и полную ссылку на Журнал Издателя.
- Автор (соавторы) гарантирует, что материалы являются оригинальной работой и представлены впервые на рассмотрение только в этом Журнале и ранее не публиковались. Если материалы написаны совместно с соавторами, автор гарантирует, что проинформировал их относительно условий публикации материалов и получил их подписи или письменное разрешение подписываться от их имени.
- Если в материалы включаются отрывки из работ или имеются указания на работы, которые охраняются авторским правом и принадлежат третьей стороне, то автору необходимо получить разрешение владельца авторских прав на использование таких материалов в первом случае и сделать ссылку на первоисточник во втором.
- Автор гарантирует, что материалы не содержат клеветнических высказываний и не посягают на права (включая без ограничений авторское право, права на патент или торговую марку) других лиц и не содержат материалы или инструкции, которые могут причинить вред или ущерб третьим лицам. Автор (каждый соавтор) гарантирует, что их публикация не приведет к разглашению секретных или конфиденциальных сведений (включая государственную тайну). Подтверждением этого является Экспертное заключение (см. перечень документов в Правила для авторов).
- Издатель обязуется опубликовать материалы в случае получения статьей положительного решения редколлегии о публикации на основании внешнего рецензирования (см. Политика рецензирования).
- В случае публикации статьи на английском языке в журнале «Radioelectronics and Communications Systems» (Издатель: Аллертон Пресс, США, распространитель Springer) автору (соавторам) выплачивается гонорар после выхода последнего номера журнала года, в котором опубликована данная статья.
- Документ Согласие на публикацию, который подают русскоязычные авторы при подаче статьи в редакцию, является краткой формой данного договора, в котором изложены все ключевые моменты настоящего договора и наличие которого подтверждает согласие автора (соавторов) с ним. Аналогичным документом для англоязычных авторов является Copyright Transfer Agreement (CTA), предоставляемый издательством Allerton Press.
- Настоящий Договор вступает в силу в момент принятия статьи к публикации. Если материалы не принимаются к публикации или до публикации в журнале автор (авторы) отозвал работу, настоящий Договор не приобретает (теряет) силу.



