Алгоритмы прямого и обратного ДКП малых порядков с уменьшенной мультипликативной сложностью

Автор(и)

  • Александр Павлович Царёв Западно-поморский технологический университет, Польща https://orcid.org/0000-0002-4513-4593
  • Марта Маковска Западно-поморский технологический университет, Польща
  • Павел Стшелец Западно-поморский технологический университет, Польща

DOI:

https://doi.org/10.20535/S0021347019110025

Ключові слова:

дискретное косинус-преобразование, ДКП, СБИС-ориентированный алгоритм, быстрые вычисления

Анотація

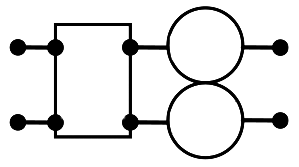
Дискретные ортогональные преобразования, такие как дискретное преобразование Фурье, дискретное преобразование Уолша, дискретное преобразование Хартли, пилоподобное преобразование, дискретное косинус-преобразование и т. д., являются важными инструментами численного анализа, обработки сигналов и статистических методов. Успешное использование этих преобразований объясняется наличием быстрых алгоритмов для их реализации. Особое место в арсенале дискретных ортогональных преобразований занимают прямое и обратное дискретное косинус-преобразование (ДКП). В статье предлагается ряд параллельных алгоритмов прямого и обратного ДКП. Их синтез основан на удачной факторизации матриц преобразования. Представлено несколько полностью параллельных алгоритмов реализации прямого и обратного ДКП малых порядков для N = {2, 3, 4, 5, 6, 7}.

Посилання

Ahmed, N.; Rao, K. R. Orthogonal Transforms for Digital Signal Processing. Springer, 1975. DOI: http://doi.org/10.1007/978-3-642-45450-9.

Elliott, Douglas F.; Rao, K. Ramamohan. Fast Transforms: Algorithms, Analyses, Applications. Academic Press, 1983.

Bi, Guoan; Zeng, Yonghong. Transforms and Fast Algorithms for Signal Analysis and Representations. Birkhäuser, 2004. DOI: http://doi.org/10.1007/978-0-8176-8220-0.

Blahut, R. E. Fast Algorithms for Digital Signal Processing. CUP, 2010. DOI: https://doi.org/10.1017/CBO9780511760921.

Ahmed, N.; Natarajan, T.; Rao, K. R. “Discrete cosine transform,” IEEE Trans. Comput., Vol. C-23, No. 1, p. 90-93, Jan. 1974. DOI: https://doi.org/10.1109/T-C.1974.223784.

Rao, K. R.; Yip, P. Discrete Cosine Transform: Algorithms, Advantages, Applications.New York: Academic Press, 1990.

Britanak, V.; Yip, P. C.; Rao, K. R. Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Amsterdam: Academic Press Inc., Elsevier Science, 2006. DOI: https://doi.org/10.1016/B978-0-12-373624-6.X5000-0.

Chitprasert, B.; Rao, K. R. “Discrete cosine transform filtering,” Signal Processing, Vol. 19, No. 3, p. 233-245, Mar. 1990. DOI: https://doi.org/10.1016/0165-1684(90)90115-F.

Ochoa-Dominguez, Humberto; Rao, K. R. Discrete Cosine Transform, 2nd ed. CRC Press, 2019.

Salomon, D. Data Compression: The Complete Reference, 3rd ed. Springer, 2004. DOI: http://doi.org/10.1007/978-1-84628-603-2.

Sayood, K. Introduction to Data Compression, 5th ed. Elsevier, 2006. URI: https://www.elsevier.com/books/introduction-to-data-compression/sayood/978-0-12-809474-7.

Puschel, M.; Moura, J. M. F. “Algebraic signal processing theory: Cooley-Tukey type algorithms for DCTs and DSTs,” IEEE Trans. Signal Process., Vol. 56, No. 4, p. 1502-1521, April 2008. DOI: https://doi.org/10.1109/TSP.2007.907919.

Chang, S. F.; Messerschmitt, D. G. “A new approach to decoding and compositing motion-compensated DCT-based images,” Proc. of IEEE ICASSP, 27-30 Apr. 1993, Minneapolis, USA. IEEE, 1993. DOI: https://doi.org/10.1109/ICASSP.1993.319837.

Krikor, L.; Baba, S.; Arif, T.; Shaaban, Z. “Image encryption using DCT and stream cipher,” European J. Sci. Res., Vol. 32, No. 1, p. 48-58, 2009.

Ptáček, M. “Digitální zpracování a přenos obrazové informace,” Nakladatelství dopravy a spojů. Praha: NADAS, 1983.

Benoit, Herve. Digital Television, 2nd ed. Focal Press, 2002. URI: https://www.oreilly.com/library/view/digital-television-2nd/9780240516950/.

Fischer, W. Digital Television: A Practical Guide for Engineers. Springer Science & Business Media, 2004. DOI: http://doi.org/10.1007/978-3-662-05429-1.

Arnold, J.; Frater, M.; Pickering, M. Digital Television: Technology and Standards, 1st ed. Wiley-Interscience, 2007. URI: https://www.wiley.com/en-us/Digital+Television%3A+Technology+and+Standards-p-9780470173411.

Hernandez, J. R.; Amado, M.; Perez-Gonzalez, F. “DCT-domain watermarking techniques for still images: detector performance analysis and a new structure,” IEEE Trans. Image Process., Vol. 9, No. 1, p. 55-68, 2000. DOI: https://doi.org/10.1109/83.817598.

Bors, A. G.; Pitas, I.“Image watermarking using DCT domain constraints,” Proc. IEEE. Int. Conf. on Image Processing, 19 Sept. 1996, Lausanne, Switzerland. IEEE, 1996, p. 231-234. DOI: https://doi.org/10.1109/ICIP.1996.560426.

Suhail, M. A.; Obaidat, M. S. “Digital watermarking-based DCT and JPEG model,” IEEE Trans. Instrumentation Meas., Vol. 52, No. 5, p. 1640-1647, 2003. DOI: https://doi.org/10.1109/TIM.2003.817155.

Chu, W. C. “DCT-based image watermarking using subsampling,” IEEE Trans. Multimedia, Vol. 5, No. 1, p. 34-38, Mar. 2003. DOI: https://doi.org/10.1109/TMM.2003.808816.

Jeon, Jeonghee; Lee, Sang-Kwang; Ho, Yo-Sung. “A three-dimensional watermarking algorithm using the DCT transform of triangle strips,” Int. Workshop Digital Watermarking, IWDW 2003: Lecture Notes in Computer Science book series. LNCS, Vol. 2939, pp. 508-517. DOI: https://doi.org/10.1007/978-3-540-24624-4_41.

Chafii, Marwa; Coon, Justin P.; Hedges, Dene A. “DCT-OFDM with index modulation,” IEEE Commun. Lett., Vol. 21, No. 7, p. 1489-1492, 2017. DOI: https://doi.org/10.1109/LCOMM.2017.2682843.

Astharini, Dwi; Gunawan, Dadang. “Discrete cosine transform and pulse amplitude modulation for visible light communication with unequally powered multiple access,” Proc. of 2018 2nd Int. Conf. on Applied Electromagnetic Technology, AEMT, 9-12 Apr. 2018, Lombok, Indonesia. IEEE, 2018, pp. 1-5. DOI: https://doi.org/10.1109/AEMT.2018.8572430.

Chen, W.-H.; Smith, C.; Fralick, S. “A fast computational algorithm for the discrete cosine transform,” IEEE Trans. Commun., Vol. 25, No. 9, p. 1004-1009, 1977. DOI: https://doi.org/10.1109/TCOM.1977.1093941.

Lee, B. “A new algorithm to compute discrete cosine transform,” IEEE Trans. Acoust., Speech, Signal Processing, Vol. 32, No. 6, p. 1243-1245, Dec. 1984. DOI: https://doi.org/10.1109/TASSP.1984.1164443.

Arai, Y.; Agui, T.; Nakajima, M. “A fast DCT-SQ scheme for images,” IEICE Trans. Fundamentals Electron., Commun. Computer Sci., Vol. 71, No. 11, p. 1095-1097, 1988. URI: https://scinapse.io/papers/2062271532.

Loeffler, C.; Ligtenberg, A.; Moschytz, G. S. “Practical fast 1-D DCT algorithms with 11 multiplications,” Proc. of Int. Conf. on Acoustics, Speech, and Signal Processing, 23-26 May 1989, Glasgow, UK. IEEE, 1989, pp. 988-991. DOI: https://doi.org/10.1109/ICASSP.1989.266596.

Kok, C. W. “Fast algorithm for computing discrete cosine transform,” IEEE Trans. Signal Processing, Vol. 45, No. 3, p. 757-760, 1997. DOI: https://doi.org/10.1109/78.558495.

Feig, E.; Winograd, S. “Fast algorithms for the discrete cosine transform,” IEEE Trans. Signal Processing, Vol. 40, No. 9, p. 2174-2193, 1992. DOI: https://doi.org/10.1109/78.157218.

Tseng, B.; Miller, W. “On computing the discrete cosine transform,” IEEE Trans. Comput., Vol. C-27, No. 10, p. 966-968, 1978. DOI: https://doi.org/10.1109/TC.1978.1674977.

Makhoul, J. “A fast cosine transform in one and two dimensions,” IEEE Trans. Acoust., Speech, Signal Processing, Vol. 28, No. 1, p. 27-34, 1980. DOI: https://doi.org/10.1109/TASSP.1980.1163351.

Vetterli, M.; Nussbaumer, H. J. “Simple FFT and DCT algorithms with reduced number of operations,” Signal Process., Vol. 6, No. 4, p. 267-278, 1984. DOI: https://doi.org/10.1016/0165-1684(84)90059-8.

Malvar, H. S. “Fast computation of discrete cosine transform through fast Hartley transform,” Electron. Lett., Vol. 22, No. 7, p. 352-353, 1986. DOI: https://doi.org/10.1049/el:19860239.

Haque, M. “A two-dimensional fast cosine transform,” IEEE Trans. Acoust., Speech, Signal Processing, Vol. 33, No. 6, p. 1532-1539, 1985. DOI: https://doi.org/10.1109/TASSP.1985.1164737.

Hou, H. S. “A fast recursive algorithm for computing the discrete cosine transform,” IEEE Trans. Acoust., Speech, Signal Processing, Vol. 35, No. 10, p. 1455-1461, 1987. DOI: https://doi.org/10.1109/TASSP.1987.1165060.

Wu, H. R.; Paoloni, F. J. “The structure of vector radix fast Fourier transforms,” IEEE Trans. Acoust., Speech, Signal Processing, Vol. 37, No. 9, p. 1415-1424, 1989. DOI: https://doi.org/10.1109/29.31295.

Chan, S. C.; Ho, K. L. “Direct methods for computing discrete sinusoidal transforms,” IEEE Proc. F: Radar Signal Process., Vol. 137, No. 6, p. 433-442, Dec. 1990. DOI: https://doi.org/10.1049/ip-f-2.1990.0063.

Cho, NamIk; Lee, San Uk. “Fast algorithm and implementation of 2-D discrete cosine transform,” IEEE Trans. Circuits Syst., Vol. 38, No. 3, p. 297-305, 1991. DOI: https://doi.org/10.1109/31.101322.

Christopoulos, C. A.; Skodras, A. N. “On the computation of the fast cosine transform,” Proc. ECCTD-Circuit Theory and Design, 1993, p. 1037-1042.

Chan, Y.-H.; Siu, W.-C. “Mixed-radix discrete cosine transform,” IEEE Trans. Signal Process., Vol. 41, No. 11, p. 3157-3161, 1993. DOI: https://doi.org/10.1109/78.257281.

Chang, Yu-Tai; Wang, Chin-Liang. “A new fast DCT algorithm and its systolic VLSI implementation,” IEEE Trans. Circuits Systems II: Analog Digital Signal Processing, Vol. 44, No. 11, p. 959-962, 1997. DOI: https://doi.org/10.1109/82.644050.

Jeong, Y.; Lee, I.; Kim, H. S.; Park, K. T. “Fast DCT algorithm with fewer multiplication stages,” Electron. Lett., Vol. 34, No. 8, p. 723-724, 1998. DOI: https://doi.org/10.1049/el:19980533.

Kwak, J.; You, J. “One- and two-dimensional constant geometry fast cosine transform algorithms and architectures,” IEEE Trans. Signal Processing, Vol. 47, No. 7, p. 2023-2034, 1999. DOI: https://doi.org/10.1109/78.771049.

Takala, J.; Akopian, D.; Astola, J.; Saarinen, J. “Constant geometry algorithm for discrete cosine transform,” IEEE Trans. Signal Processing, Vol. 48, No. 6, p. 1840-1843, 2000. DOI: https://doi.org/10.1109/78.845951.

Bi, G.; Li, G.; Ma, K.-K.; Tan, T. C. “On the computation of two-dimensional DCT,” IEEE Trans. Signal Process., Vol. 48, No. 4, p. 1171-1183, Apr. 2000. DOI: https://doi.org/10.1109/78.827550.

Guo, Jiun-In. “A low cost 2-D inverse discrete cosine transform design for image compression,” Proc. of 2001 IEEE Int. Symp. on Circuits and Systems, 6-9 May 2001, Sydney, Australia. IEEE, 2001, Vol. 4, pp. 658-661. DOI: https://doi.org/10.1109/ISCAS.2001.922323.

Shao, X.; Johnson, S. G. “Type-II/III DCT/DST algorithms with reduced number of arithmetic operations,” Signal Processing, Vol. 88, No. 6, p. 1553-1564, 2008. DOI: https://doi.org/10.1016/j.sigpro.2008.01.004.

Pennebaker, W. B.; Mitchell, J. L. JPEG still Image Data Compression Standard. New York: Van Nostrand Reinhold, 1993. URI: https://www.springer.com/gp/book/9780442012724.

Lee, Pei-Zong; Huang, Fang-Yu. “An efficient prime-factor algorithm for the discrete cosine transform and its hardware implementations,” IEEE Trans. Signal Processing, Vol. 42, No. 8, p. 1996-2005, 1994. DOI: https://doi.org/10.1109/78.301838.

Tatsaki, A.; Dre, C.; Stouraitis, T.; Goutis, C. “On the computation of the prime factor DST,” Signal Processing, Vol. 42, No. 3, p. 231-236, 1995. DOI: https://doi.org/10.1016/0165-1684(94)00132-J.

Tatsaki, A.; Dre, C.; Stouraitis, T.; Goutis, C. “Prime-factor DCT algorithms,” IEEE Trans. Signal Processing, Vol. 43, No. 3, p. 772-776, 1995. DOI: https://doi.org/10.1109/78.370632.

Bi, Guoan; Zeng, Yonghong; Chen, Yen Qiu. “Prime factor algorithm for multidimensional discrete cosine transform,” IEEE Trans. Signal Processing, Vol. 49, No. 9, p. 2156-2161, 2001. DOI: https://doi.org/10.1109/78.942642.

Lu, S.-K.; Wu, C.-W.; Juo, S.-Y. “Design of easily testable VLSI arrays for discrete cosine transform,” Proc. of Twenty-Sixth Asilomar Conf. on Signals Systems and Computers, 26-28 Oct. 1992. Pacific Grove, USA. IEEE, 1992, Vol. 2, pp. 989-993. DOI: https://doi.org/10.1109/ACSSC.1992.269072.

Lee, S.-W.; Hsu, W.-H. “Parallel implementation of prime-factor discrete cosine transform on the orthogonal multiprocessor,” IEEE Trans. Circuits Systems Video Technol., Vol. 3, No. 2, p. 107-115, 1993. DOI: https://doi.org/10.1109/76.212717.

Murthy, N. Rama; Swamy, M. N. S. “On the real-time computation of DFT and DCT through systolic architectures,” IEEE Trans. Signal Processing, Vol. 42, No. 4, p. 988-991, 1994. DOI: https://doi.org/10.1109/78.285671.

Shin, K.-W.; Jeon, H.-W.; Kang, Y.-S. “An efficient VLSI implementation of vector-radix 2-D DCT using mesh-connected 2-D array,” Proc. of IEEE Int. Symp. on Circuits and Systems, 30 May-2 June 1994, London, UK. IEEE, 1994, Vol. 4, pp. 47-50. DOI: https://doi.org/10.1109/ISCAS.1994.409193.

Wang, Chin-Liang; Chen, Chang-Yu. “High-throughput VLSI architectures for the 1-D and 2-D discrete cosine transforms,” IEEE Trans. Circuits Systems Video Technology, Vol. 5, No. 1, p. 31-40, 1995. DOI: https://doi.org/10.1109/76.350776.

Hsia, Shih-Chang; Liu, Bin-Da; Yang, Jar-Ferr; Bai, Bor-Long. “VLSI implementation of parallel coefficient-by-coefficient two-dimensional IDCT processor,” IEEE Trans. Circuits Systems Video Technology, Vol. 5, No. 5, p. 396-406, 1995. DOI: https://doi.org/10.1109/76.473561.

Lim, Hyesook; Swartzlander, E. E. “An efficient systolic array for the discrete cosine transform based on prime-factor decomposition,” Proc. of 1995 Int. Conf. on Computer Design. VLSI in Computers and Processors, 2-4 Oct. 1995, Austin, USA. IEEE, 1995, pp. 644-649. DOI: https://doi.org/10.1109/ICCD.1995.528936.

Chang, Yu-Tai; Wang, Chin-Liang. “Systolic architecture for inverse discrete cosine transform,” Electron. Lett., Vol. 31, No 21, p. 1809-1811, 1995. URI: https://ieeexplore.ieee.org/abstract/document/8840699.

Madisetti, A.; Willson, A. N. “A 100 MHz 2-D 8ґ8 DCT/IDCT processor for HDTV applications,” IEEE Trans. Circuits Systems Video Technol., Vol. 5, No. 2, p. 158-165, 1995. DOI: https://doi.org/10.1109/76.388064.

Srinivasan, V.; Liu, K. J. R. “VLSI design of high-speed time-recursive 2-D DCT/IDCT processor for video applications,” IEEE Trans. Circuits Syst. Video Technol., Vol. 6, No. 1, p. 87-96, 1996. DOI: https://doi.org/10.1109/76.486423.

Schimpfle, C. V.; Rieder, P.; Nossek, J. A. “A power efficient implementation of the discrete cosine transform,” Proc. of Thirty-First Asilomar Conf. on Signals, Systems and Computers, 2-5 Nov. 1997, Pacific Grove, USA. IEEE, 1997, Vol. 1, pp. 729-733. DOI: https://doi.org/10.1109/ACSSC.1997.680540.

Lee, Y.-P.; Chen, T.-H.; Chen, L.-G.; Chen, M.-J.; Ku, C.-W. “A cost-effective architecture for 8×8 two-dimensional DCT/IDCT using direct method,” IEEE Trans. Circuits Syst. Video Technol., Vol. 7, No. 3, p. 459-467, 1997. DOI: https://doi.org/10.1109/76.585925.

Chang, Yu-Tai; Wang, Chin-Liang. “A new fast DCT algorithm and its systolic VLSI implementation,” IEEE Trans. Circuits Systems II: Analog Digital Signal Processing, Vol. 44, No. 11, p. 959-962, 1997. DOI: https://doi.org/10.1109/82.644050.

BenAyed, M. A.; Dulau, L.; Nouel, P.; Berthoumieu, Y.; Masmoudi, N.; Kadionik, P.; Kamoun, L. “New design using a VHDL description for DCT based circuits,” Proc. of ICM’98, 16 Dec. 1998, Monastir, Tunisia. IEEE, 1998, pp. 87-90. DOI: https://doi.org/10.1109/ICM.1998.825575.

Chen, L.-G.; Jiu, J.-Y.; Chang, H.-C.; Lee, Y.-P.; Ku, C.-W. “A low power 2D DCT chip design using direct 2D algorithm,” Proc. of Asia and South Pacific Design Automation Conf., 13 Feb. 1998, Yokohama, Japan. IEEE, 1998, pp. 145-150. DOI: https://doi.org/10.1109/ASPDAC.1998.669434.

Lu, Chung-Yen; Wen, Kuei-Ann. “On the design of selective coefficient DCT module,” IEEE Trans. Circuits Systems Video Technology, Vol. 8, No. 2, p. 143-146, 1998. DOI: https://doi.org/10.1109/76.664099.

Hsiao, S.-F.; Shiue, W.-R.; Tseng, J.-M. “A cost-efficient and fully-pipelinable architecture for DCT/IDCT,” IEEE Trans. Consumer Electron., Vol. 45, No. 3, p. 515-525, 1999. DOI: https://doi.org/10.1109/30.793535.

Kim, K.; Koh, J.-S. “An area efficient DCT architecture for MPEG-2 video encoder,” IEEE Trans. Consumer Electron., Vol. 45, No. 1, p. 62-67, 1999. DOI: https://doi.org/10.1109/30.754418.

Chang, T.-S.; Kung, C.-S.; Jen, C.-W. “A simple processor core design for DCT/IDCT,” IEEE Trans. Circuits Syst. Video Technol., Vol. 10, No. 3, p. 439-447, 2000. DOI: https://doi.org/10.1109/76.836290.

Lim, Hyesook; Piuri, V.; Swartzlander, E. E. “A serial-parallel architecture for two-dimensional discrete cosine and inverse discrete cosine transforms,” IEEE Trans. Computers, Vol. 49, No. 12, p. 1297-1309, 2000. DOI: https://doi.org/10.1109/12.895848.

Jiang, Min; Luo, Yuan; Fu, Yiling; Yang, Bing; Zhao, Baoying; Wang, Xin-an; Sheng, Shimin; Zhang, Tianyi. “A low power 1D-DCT processor for MPEG-targeted real-time applications,” Proc. of IEEE Int. Symp. on Communications and Information Technology, 26-29 Oct. 2004, Sapporo, Japan. IEEE, 2004, Vol. 2, pp. 682-687. DOI: https://doi.org/10.1109/ISCIT.2004.1413802.

Mohanty, S. P.; Ranganathan, N.; Balakrishnan, K. “A dual voltage-frequency VLSI chip for image watermarking in DCT domain,” IEEE Trans. Circuits Syst. II Exp. Briefs, Vol. 53, No. 5, p. 394-398, 2006. DOI: https://doi.org/10.1109/TCSII.2006.870216.

Qureshi, F.; Garrido, M.; Gustafsson, O. “Unified architecture for 2, 3, 4, 5, and 7-point DFTs based on Winograd Fourier transform algorithm,” Electron. Lett., Vol. 49, No. 5, p. 348-349, 2013. DOI: https://doi.org/10.1049/el.2012.0577.

De Oliveira, H. M.; Cintra, R. J.; Campello de Souza, R. M. “A factorization scheme for some discrete Hartley transform matrices,” 1-10, 2015. arXiv:1502.01038.

Cariow, A.; Papliński, J.; Majorkowska-Mech, D. “Some structures of parallel VLSI-oriented processing units for implementation of small size discrete fractional Fourier transforms,” Electronics, Vol. 8, No. 5, p. 509, 2019. DOI: https://doi.org/10.3390/electronics8050509.

Reznik, Yu. A.; Chivukula, Ravi K. “Design of fast transforms for high-resolution image and video coding,” Proc. SPIE 7443, Applications of Digital Image Processing XXXII, 744312 (2 Sept. 2009). DOI: http://doi.org/10.1117/12.831216.

Britanak, V.; Rao, K. R. Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations. Springer, 2018. DOI: https://doi.org/10.1007/978-3-319-61080-1.

Tran, Trac D.; Liang, Jie; Tu, Chengjie. “Lapped transform via time-domain pre- and post-filtering,” IEEE Trans. Signal Processing, Vol. 51, No. 6, p. 1557-1571, 2003. DOI: https://doi.org/10.1109/TSP.2003.811222.

Ţariov, A.; Majorkowska-Mech, D. “The multilevel signal representation in discrete base of cosine functions,” Elektronika: konstrukcje technologie zastosowania, Vol. 48, No. 7, p. 20-21, 2007.

Chernov, V. M.; Chicheva, M. A. “One-step’ short-length DCT algorithms with data representation in the direct sum of the associative algebras,” in: Sommer, G.; Daniilidis, K.; Pauli, J. (eds.), Computer Analysis of Images and Patterns. CAIP 1997. Lecture Notes in Computer Science, 1997, Vol. 1296. pp. 590-596, Springer, Berlin, Heidelberg. DOI: https://doi.org/10.1007/3-540-63460-6_167.

Ţariov, A. Algorytmiczne aspekty racjonalizacji obliczeń w cyfrowym przetwarzaniu sygnałów (in Polish) [Algorithmic aspects of computing rationalization in Digital Signal processing].WestPomeranianUniversity Press, 2012.

Cariow, A. “Strategies for the synthesis of fast algorithms for the computation of the matrix-vector products,” J. Signal Processing Theory Applications, No. 3, p. 1-19, 2014. DOI: http://doi.org/10.7726/jspta.2014.1001.

Graham, A. Kronecker Products and Matrix Calculus: With Applications.Chichester,England: Ellis Horwood Limited, 1981.

Regalia, P. A.; Mitra, S. K. “Kronecker products, unitary matrices and signal processing applications,” SIAM Review, Vol. 31, No. 4, p. 586-613, 1989. DOI: https://doi.org/10.1137/1031127.

Granata, J.; Conner, M.; Tolimieri, R. “The tensor product: A mathematical programming language for FFTs and other fast DSP operations,” IEEE Signal Process. Mag., Vol. 9, No. 1, p. 40-48, 1992. DOI: https://doi.org/10.1109/79.109206.

##submission.downloads##

Опубліковано

2019-11-22

Як цитувати

Царёв, А. П., Маковска, М., & Стшелец, П. (2019). Алгоритмы прямого и обратного ДКП малых порядков с уменьшенной мультипликативной сложностью. Вісті вищих учбових закладів. Радіоелектроніка, 62(11), 662–677. https://doi.org/10.20535/S0021347019110025

Номер

Том 62 № 11 (2019)

Розділ

Оригінальні статті

Ліцензія

Авторське право (c) 2019 Известия высших учебных заведений. Радиоэлектроника

Издатель журнала Известия высших учебных заведений. Радиоэлектроника (сокр. "Известия вузов. Радиоэлектроника"), Национальный технический университет Украины "Киевский политехнический институт", учитывает, что доступ автора к его статье является важным как для самого автора, так и для спонсоров его исследований. Мы представлены в базе издателей SHERPA/RoMEO как зеленый издатель (green publisher), что позволяет автору выполнять самоархивирование своей статьи. Однако важно, чтобы каждая из сторон четко понимала свои права. Просьба более детально ознакомиться с Политикой самоархивирования нашего журнала.

Политика оплаченного открытого доступа POA (paid open access), принятая в журнале, позволяет автору выполнить все необходимые требования по открытому доступу к своей статье, которые выдвигаются институтом, правительством или фондом при выделении финансирования. Просьба более детально ознакомиться с политикой оплаченного открытого доступа нашего журнала (см. отдельно).

Варианты доступа к статье:

1. Статья в открытом доступе POA (paid open access)

В этом случае права автора определяются лицензией CC BY (Creative Commons Attribution).

2. Статья с последующим доступом по подписке

В этом случае права автора определяются авторским договором, приведенным далее.

  • Автор (каждый соавтор) уступает Издателю журнала «Известия высших учебных заведений. Радиоэлектроника» НТУУ «КПИ» на срок действия авторского права эксклюзивные права на материалы статьи, в том числе право на публикацию данной статьи издательством Аллертон Пресс, США (Allerton Press) на английском языке в журнале «Radioelectronics and Communications Systems». Передача авторского права охватывает исключительное право на воспроизведение и распространение статьи, включая оттиски, переводы, фото воспроизведения, микроформы, электронные формы (он- и оффлайн), или любые иные подобные формы воспроизведения, а также право издателя на сублицензирование третьим лицам по своему усмотрению без дополнительных консультаций с автором. При этом журнал придерживается Политики конфиденциальности.
  • Передача прав включает право на обработку формы представления материалов с помощью компьютерных программам и систем (баз данных) для их использования и воспроизводства, публикации и распространения в электронном формате и внедрения в системы поиска (базы данных).
  • Воспроизведение, размещение, передача или иное распространение или использование материалов, содержащихся в статье должно сопровождаться ссылкой на Журнал и упоминанием Издателя, а именно: название статьи, имя автора (соавторов), название журнала, номер тома, номер выпуска, копирайт авторов и издателя "© Национальный технический университет Украины "Киевский политехнический институт"; © автор(ы)".
  • Автор (каждый соавтор) материалов сохраняет все права собственника материалов, включая патентные права на любые процессы, способы или методы и др., а также права на товарные знаки.
  • Издатель разрешает автору (каждому соавтору) материалов следующее:
  1. Право пользоваться печатными или электронными вариантами материалов статьи в форме и содержании, принятыми Издателем для публикации в Журнале. Подробнее см. политики Оплаченного открытого доступа, подписки и самоархивирования.
  2. Право бесплатно копировать или передавать коллегам копию напечатанной статьи целиком или частично для их личного или профессионального использования, для продвижения академических или научных исследований или для учебного процесса или других информационных целей, не связанных с коммерческими целями.
  3. Право использовать материалы из опубликованной статьи в написанной автором (соавторами) книге, монографии, учебнике, учебном пособии и других научных и научно-популярных изданиях.
  4. Право использовать отдельные рисунки или таблицы и отрывки текста из материалов в собственных целях обучения или для включения их в другую работу, которая печатается (в печатном или электронном формате) третьей стороной, или для представления в электронном формате во внутренние компьютерные сети или на внешние сайты автора (соавторов).
  • Автор (соавторы) соглашаются, что каждая копия материалов или любая ее часть, распространенная или размещенная ими в печатном или электронном формате, будет содержать указание на авторское право, предусмотренное в Журнале и полную ссылку на Журнал Издателя.
  • Автор (соавторы) гарантирует, что материалы являются оригинальной работой и представлены впервые на рассмотрение только в этом Журнале и ранее не публиковались. Если материалы написаны совместно с соавторами, автор гарантирует, что проинформировал их относительно условий публикации материалов и получил их подписи или письменное разрешение подписываться от их имени.
  • Если в материалы включаются отрывки из работ или имеются указания на работы, которые охраняются авторским правом и принадлежат третьей стороне, то автору необходимо получить разрешение владельца авторских прав на использование таких материалов в первом случае и сделать ссылку на первоисточник во втором.
  • Автор гарантирует, что материалы не содержат клеветнических высказываний и не посягают на права (включая без ограничений авторское право, права на патент или торговую марку) других лиц и не содержат материалы или инструкции, которые могут причинить вред или ущерб третьим лицам. Автор (каждый соавтор) гарантирует, что их публикация не приведет к разглашению секретных или конфиденциальных сведений (включая государственную тайну). Подтверждением этого является Экспертное заключение (см. перечень документов в Правила для авторов).
  • Издатель обязуется опубликовать материалы в случае получения статьей положительного решения редколлегии о публикации на основании внешнего рецензирования (см. Политика рецензирования).
  • В случае публикации статьи на английском языке в журнале «Radioelectronics and Communications Systems» (Издатель: Аллертон Пресс, США, распространитель Springer) автору (соавторам) выплачивается гонорар после выхода последнего номера журнала года, в котором опубликована данная статья.
  • Документ Согласие на публикацию, который подают русскоязычные авторы при подаче статьи в редакцию, является краткой формой данного договора, в котором изложены все ключевые моменты настоящего договора и наличие которого подтверждает согласие автора (соавторов) с ним. Аналогичным документом для англоязычных авторов является Copyright Transfer Agreement (CTA), предоставляемый издательством Allerton Press.
  • Настоящий Договор вступает в силу в момент принятия статьи к публикации. Если материалы не принимаются к публикации или до публикации в журнале автор (авторы) отозвал работу, настоящий Договор не приобретает (теряет) силу.