Преимущества новой стратегии для процессоров CFAR по сравнению с моделью Неймана-Пирсона при обнаружении флуктуирующих целей, описываемых распределением хи-квадрат с четырьмя степенями свободы

Автор(и)

DOI:

https://doi.org/10.20535/S0021347018090017

Ключові слова:

адаптивный процессор, мешающие отражения, клаттер, помеха, , распределение хи-квадрат, модель SWIII, модель SWIV, некогерентное интегрирование, среда с групповыми целями

Анотація

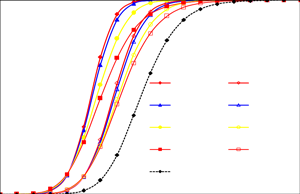
Современные радары «приняли на вооружение» и используют методики адаптивной обработки для ослабления неблагоприятного влияния нежелательных мешающих отражений (clutter) и постановщиков помех (jammer). В такой ситуации алгоритмы обнаружения с постоянной вероятностью ложных тревог CFAR (Constant False Alarm Rate) играют важную роль при обнаружении флуктуирующих целей в неоднородной среде. При этом, хотя процессор с усредненной по ячейке вероятностью ложных тревог CA-CFAR (Cell-Averaging CFAR) имеет лучшие характеристики в однородной среде, методики порядковой статистики OS (Order Statistics) и усеченной по среднему значению TM (Trimmed-Mean) предложены для обеспечения устойчивых оценок порога в условиях неоднородной среды. Для одновременного использования достоинств процессора CA и процессора OS или TM в последнее время предложены их гибридные варианты. Они получили название моделей CAOS и CATM. Практически, частотное разнесение между несвязанными зондированиями широко распространено в реальных радиолокационных системах. Кроме того, стратегия интегрирования импульсов часто используется в радиолокационных системах для повышения отношения сигнал–шум SNR цели и улучшения характеристик обнаружения системы. Поэтому в данной работе основное внимание уделено анализу этих новых моделей в случае, когда радиолокационный приемник некогерентно интегрирует  М-импульсы при обнаружении. Для их рабочих характеристик в условиях неоднородной среды получено выражение в замкнутой форме. Предполагается, что искомая и ложная цели описываются χ2 распределением с четырьмя степенями свободы их флуктуаций. Результаты моделирования, полученные авторами, показывают, что новая версия модели CATM демонстрирует рабочую характеристику в условиях однородной среды, которая превосходит таковую для классической процедуры Неймана–Пирсона, используемую в качестве стандартной при сравнении других стратегий в области адаптивных обнаружителей.

Посилання

Weiner, M. A. “Detection probability for partially correlated chi-square targets,” IEEE Trans. Aerospace Electronic Systems, Vol. 24, No. 4, p. 411-416, 1988. DOI: https://doi.org/10.1109/7.7183.

Barkat, M.; Himonas, S. D.; Varshney, P. K. “CFAR detection for multiple target situations,” IEE Proc. F - Radar Signal Processing, Vol. 136, No. 5, p. 193-209, 1989. DOI: https://doi.org/10.1049/ip-f-2.1989.0033.

El Mashade, M. B. “Detection performance of the trimmed-mean CFAR processor with noncoherent integration,” IEE Proc. Radar, Sonar Navig., Vol. 142, No. 1, p. 18-24, 1995. DOI: https://doi.org/10.1049/ip-rsn:19951626.

Nagle, Daniel T.; Saniie, Jafar. “Performance analysis of linearly combined order statistic CFAR detectors,” IEEE Trans. Aerospace Electronic Systems, Vol. 31, No. 2, p. 522-533, 1995. DOI: https://doi.org/10.1109/7.381903.

Han, D.-S. “Detection performance of CFAR detectors based on order statistics for partially correlated chi-square targets,” IEEE Trans. Aerospace Electronic Systems, Vol. 36, No. 4, p. 1423-1429, 2000. DOI: https://doi.org/10.1109/7.892694.

Farrouki, A.; Barkat, M. “Automatic censoring CFAR detector based on ordered data variability for nonhomogeneous environments,” IEE Proc. - Radar Sonar Navig., Vol. 152, No. 1, p. 43-51, 2005. DOI: https://doi.org/10.1049/ip-rsn:20045006.

El Mashade, M. B. “Analysis of cell-averaging based detectors for χ2 fluctuating targets in multitarget environments,” J. Electron. (China), Vol. 23, No. 6, p. 853-863, 2006. DOI: https://doi.org/10.1007/s11767-005-0067-0.

Laroussi, T.; Barkat, M. “A performance comparison of two time diversity systems using CMLD-CFAR detection for partially-correlated chi-square targets and multiple target situations,” Proc. of 14th European Signal Processing Conf., 4-8 Sept. 2006, Florence, Italy. IEEE, 2006, pp. 4-8, URI: https://ieeexplore.ieee.org/document/7071138.

El Mashade, M. B. “Performance analysis of OS structure of CFAR detectors in fluctuating target environments,” PIER C, Vol. 2, p. 127-158, 2008. DOI: https://doi.org/10.2528/PIERC08022807.

Magaz, B.; Belouchrani, A.; Hamadouche, M. “A new adaptive linear combined CFAR detector in presence of interfering targets,” PIER B, Vol. 34, p. 367-387, 2011. DOI: http://doi.org/10.2528/PIERB11012603.

Cai, Long; Ma, Xiaochuan; Xu, Qi; Li, Bin; Ren, Shiwei. “Performance analysis of some new CFAR detectors under clutter,” J. Computers, Vol. 6, No. 6, p. 1278-1285, 2011. DOI: http://doi.org/10.4304/jcp.6.6.1278-1285.

Wang, W. Q. Radar Systems: Technology, Principles and Applications. Nova Science Publishers, Inc, 2013.

Ivković, Dejan; Andrić, Milenko; Zrnić, Bojan. “A new model of CFAR detector,” Frequenz, Vol. 68, No. 3-4, p. 125-136, 2014. DOI: https://doi.org/10.1515/freq-2013-0087.

Ivković, Dejan; Andrić, Milenko; Zrnić, Bojan. “False alarm analysis of the CATM-CFAR in presence of clutter edge,” Radioengineering, Vol. 23, No. 1, p. 66-72, 2014. URI: http://www.radioeng.cz/fulltexts/2014/14_01_0066_0072.pdf.

El Mashade, M. B. “Partially-correlated χ2 targets detection analysis of GTM-adaptive processor in the presence of outliers,” Int. J. Image, Graphics Signal Processing, Vol. 7, No. 12, p. 70-90, 2014. DOI: http://doi.org/10.5815/ijigsp.2014.12.10.

Ivković, Dejan; Andrić, Milenko; Zrnić, Bojan; Okiljević, Predrag; Kozić, Nadica. “CATM-CFAR detector in the receiver of the software defined radar,” Sci. Tech. Rev., Vol. 54, No. 4, p. 27-38, 2014. URI: http://www.vti.mod.gov.rs/ntp/rad2014/4-2014/3/e3.htm.

Ahmed, S. “Novel noncoherent radar pulse integration to combat noise jamming,” IEEE Trans. Aerospace Electronic Systems, Vol. 51, No. 3, p. 2350-2359, 2015. DOI: https://doi.org/10.1109/TAES.2015.140315.

Ivković, Dejan; Andrić, Milenko; Zrnić, Bojan. “Detection of very close targets by fusion CFAR detectors,” Sci. Tech. Rev., Vol. 66, No. 3, p. 50-57, 2016. DOI: https://doi.org/10.5937/STR1603050I.

Machado-Fernandez, J. R.; Mojena-Hernandez, N.; Bacallao-Vidal, J. C. “Evaluation of CFAR detectors performance,” Iteckne, Vol. 14, No. 2, p. 170-178, 2017. DOI: http://dx.doi.org/10.15332/iteckne.v14i2.1772.

Islam, M. M.; Hossam-E-Haider, M. “Detection capability and CFAR loss under fluctuating targets of different Swerling model for various gamma parameters in RADAR,” Int. J. Advanced Computer Science Applications, Vol. 9, No. 2, p. 90-93, 2018. DOI: http://dx.doi.org/10.14569/IJACSA.2018.090214.

El Mashade, M. B. “Heterogeneous performance analysis of the new model of CFAR detectors for partially-correlated χ2-targets,” J. Systems Engineering Electronics, Vol. 29, No. 1, p. 1-17, 2018. DOI: https://doi.org/10.21629/JSEE.2018.01.01.

##submission.downloads##

Опубліковано

2018-09-28

Як цитувати

Эль Машад, М. Б. (2018). Преимущества новой стратегии для процессоров CFAR по сравнению с моделью Неймана-Пирсона при обнаружении флуктуирующих целей, описываемых распределением хи-квадрат с четырьмя степенями свободы. Вісті вищих учбових закладів. Радіоелектроніка, 61(9), 487–507. https://doi.org/10.20535/S0021347018090017

Номер

Том 61 № 9 (2018)

Розділ

Оригінальні статті

Ліцензія

Авторське право (c) 2018 Известия высших учебных заведений. Радиоэлектроника

Издатель журнала Известия высших учебных заведений. Радиоэлектроника (сокр. "Известия вузов. Радиоэлектроника"), Национальный технический университет Украины "Киевский политехнический институт", учитывает, что доступ автора к его статье является важным как для самого автора, так и для спонсоров его исследований. Мы представлены в базе издателей SHERPA/RoMEO как зеленый издатель (green publisher), что позволяет автору выполнять самоархивирование своей статьи. Однако важно, чтобы каждая из сторон четко понимала свои права. Просьба более детально ознакомиться с Политикой самоархивирования нашего журнала.

Политика оплаченного открытого доступа POA (paid open access), принятая в журнале, позволяет автору выполнить все необходимые требования по открытому доступу к своей статье, которые выдвигаются институтом, правительством или фондом при выделении финансирования. Просьба более детально ознакомиться с политикой оплаченного открытого доступа нашего журнала (см. отдельно).

Варианты доступа к статье:

1. Статья в открытом доступе POA (paid open access)

В этом случае права автора определяются лицензией CC BY (Creative Commons Attribution).

2. Статья с последующим доступом по подписке

В этом случае права автора определяются авторским договором, приведенным далее.

  • Автор (каждый соавтор) уступает Издателю журнала «Известия высших учебных заведений. Радиоэлектроника» НТУУ «КПИ» на срок действия авторского права эксклюзивные права на материалы статьи, в том числе право на публикацию данной статьи издательством Аллертон Пресс, США (Allerton Press) на английском языке в журнале «Radioelectronics and Communications Systems». Передача авторского права охватывает исключительное право на воспроизведение и распространение статьи, включая оттиски, переводы, фото воспроизведения, микроформы, электронные формы (он- и оффлайн), или любые иные подобные формы воспроизведения, а также право издателя на сублицензирование третьим лицам по своему усмотрению без дополнительных консультаций с автором. При этом журнал придерживается Политики конфиденциальности.
  • Передача прав включает право на обработку формы представления материалов с помощью компьютерных программам и систем (баз данных) для их использования и воспроизводства, публикации и распространения в электронном формате и внедрения в системы поиска (базы данных).
  • Воспроизведение, размещение, передача или иное распространение или использование материалов, содержащихся в статье должно сопровождаться ссылкой на Журнал и упоминанием Издателя, а именно: название статьи, имя автора (соавторов), название журнала, номер тома, номер выпуска, копирайт авторов и издателя "© Национальный технический университет Украины "Киевский политехнический институт"; © автор(ы)".
  • Автор (каждый соавтор) материалов сохраняет все права собственника материалов, включая патентные права на любые процессы, способы или методы и др., а также права на товарные знаки.
  • Издатель разрешает автору (каждому соавтору) материалов следующее:
  1. Право пользоваться печатными или электронными вариантами материалов статьи в форме и содержании, принятыми Издателем для публикации в Журнале. Подробнее см. политики Оплаченного открытого доступа, подписки и самоархивирования.
  2. Право бесплатно копировать или передавать коллегам копию напечатанной статьи целиком или частично для их личного или профессионального использования, для продвижения академических или научных исследований или для учебного процесса или других информационных целей, не связанных с коммерческими целями.
  3. Право использовать материалы из опубликованной статьи в написанной автором (соавторами) книге, монографии, учебнике, учебном пособии и других научных и научно-популярных изданиях.
  4. Право использовать отдельные рисунки или таблицы и отрывки текста из материалов в собственных целях обучения или для включения их в другую работу, которая печатается (в печатном или электронном формате) третьей стороной, или для представления в электронном формате во внутренние компьютерные сети или на внешние сайты автора (соавторов).
  • Автор (соавторы) соглашаются, что каждая копия материалов или любая ее часть, распространенная или размещенная ими в печатном или электронном формате, будет содержать указание на авторское право, предусмотренное в Журнале и полную ссылку на Журнал Издателя.
  • Автор (соавторы) гарантирует, что материалы являются оригинальной работой и представлены впервые на рассмотрение только в этом Журнале и ранее не публиковались. Если материалы написаны совместно с соавторами, автор гарантирует, что проинформировал их относительно условий публикации материалов и получил их подписи или письменное разрешение подписываться от их имени.
  • Если в материалы включаются отрывки из работ или имеются указания на работы, которые охраняются авторским правом и принадлежат третьей стороне, то автору необходимо получить разрешение владельца авторских прав на использование таких материалов в первом случае и сделать ссылку на первоисточник во втором.
  • Автор гарантирует, что материалы не содержат клеветнических высказываний и не посягают на права (включая без ограничений авторское право, права на патент или торговую марку) других лиц и не содержат материалы или инструкции, которые могут причинить вред или ущерб третьим лицам. Автор (каждый соавтор) гарантирует, что их публикация не приведет к разглашению секретных или конфиденциальных сведений (включая государственную тайну). Подтверждением этого является Экспертное заключение (см. перечень документов в Правила для авторов).
  • Издатель обязуется опубликовать материалы в случае получения статьей положительного решения редколлегии о публикации на основании внешнего рецензирования (см. Политика рецензирования).
  • В случае публикации статьи на английском языке в журнале «Radioelectronics and Communications Systems» (Издатель: Аллертон Пресс, США, распространитель Springer) автору (соавторам) выплачивается гонорар после выхода последнего номера журнала года, в котором опубликована данная статья.
  • Документ Согласие на публикацию, который подают русскоязычные авторы при подаче статьи в редакцию, является краткой формой данного договора, в котором изложены все ключевые моменты настоящего договора и наличие которого подтверждает согласие автора (соавторов) с ним. Аналогичным документом для англоязычных авторов является Copyright Transfer Agreement (CTA), предоставляемый издательством Allerton Press.
  • Настоящий Договор вступает в силу в момент принятия статьи к публикации. Если материалы не принимаются к публикации или до публикации в журнале автор (авторы) отозвал работу, настоящий Договор не приобретает (теряет) силу.